不用猜 你那排列组合还在那比划半天
先来看一个简单的例子:
从列表{1..5}中选出2个数的所有组合如下所示:
(1,2)、(1,3)、(1,4)、(1,5)、(2,3)、(2,4)、(2,5)、(3,4)、(3,5)、(4,5)
power query的解决方案是:
List.TransformMany({1..5},each {_+1..5},(a,b)=>a*10+b)或者用list表示
List.TransformMany({1..5},each {_+1..5},(a,b)=>{a,b})
如果我们的列表是文本或混合数据可以
[L={"A","畅心","B","施阳",2},P=List.TransformMany({0..3},each {_+1..4},(a,b)=>{L{a},L{b}})][P]
//L作为重复引用列表,我们可以用List.Buffer缓存起来、提高引用效率。有人就问了,两个的组合好搞,那要三个以上怎么办呢?
假设t1=List.TransformMany({1..5},each {_+1..5},(a,b)=>{a,b})
按照组合逻辑从两个的组合升级到三个一组为:
(1,2)==》(1,2,3)、(1,2,4)、(1,2,5)
(1,3)==》(1,3,4)、(1,3,5)
(1,4)==》(1,4,5)
(1,5)==》(1,5,6)X
(2,3)==》(2,3,4)、(2,3,5)
(2,4)==》(2,4,5)
(2,5)==》(2,5,6)X
(3,4)==》(3,4,5)
(3,5)==》(3,5,6)X
(4,5)==》(4,5,6)X
规律就是将两个的组合中每组各自加入大于每组中最后那个数字的列表元素即可。
List.TransformMany(t1,each {List.Last(_)+1..5},(a,b)=>a&{b})注意这里就应用了映射的特性剔除不需要的组合,比如(1,5)根据映射规则产生{6..5},由于该映射值本身不存在,故映射不到具体值,List.TransformMany函数将不会产生该组合!
那么统一为一个公式就是:
List.Accumulate({1,2},List.Zip({{1..5}}),(x,y)=>List.TransformMany(x,each {List.Last(_)+1..5},(a,b)=>a&{b}))或者
List.Accumulate({1,2},List.Zip({{1..5}}),(x,y)=>List.TransformMany(x,each {_{y-1}+1..5},(a,b)=>a&{b}))这里List.Zip({{1..5}})为了产生初始列表{{1},{2},{3},{4},{5}},让初始值满足后面映射统一构建需要,同时统一了组合的初始容器结构、这样方便让后续元素装进各自组合进行统一运算。
用35选7试试水,死机了吗?
List.Accumulate({1..6},List.Zip({{1..35}}),(x,y)=>List.TransformMany(x,each {List.Last(_)+1..35},(a,b)=>a&{b}))或者
List.Accumulate({1..6},List.Zip({{1..35}}),(x,y)=>List.TransformMany(x,each {_{y-1}+1..35},(a,b)=>a&{b}))当然考虑实际情况35选7最后一次迭代只需要从29开始映射即可:
List.Accumulate({0..5},List.Zip({{1..29}}),(x,y)=>
List.TransformMany(x,each {_{y}+1..35},(a,b)=>a&{b}))有个小例子,男女搭配分组5男={"A".."E"},5女={"M".."Q"},随机将他们分成5组,每组一男一女:
逻辑就是你随便打乱其中一组然后List.Zip组合即可,可能在表中引用随机序列不稳定需要List.Buffer缓存一下。
当然这里的组合均是不重复的,有的时候获取我们要的是排列即(1,2)和(2,1)两个组合代表不同意义均要求获取,这种情形反而更容易获取,最典型的就是笛卡尔积的应用。
我们在power query中有个单列的表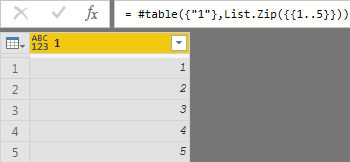
这里产生笛卡尔积很简单,插入一个自定义列{1..5}即可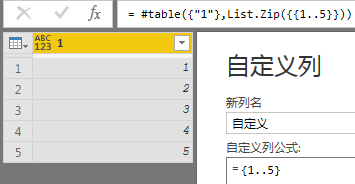
展开、你可以剔除组合中相同的元素行。
当然,我不喜欢在表结构里面手动去加自定义列:
List.TransformMany({1..5},each List.RemoveRange({1..5},_-1),(x,y)=>{x,y})
然后又有人要问两个以上的排列呢?
提示一下还有个函数:List.RemoveItems
对于大量元素的列表的数据组合,可能生成超大组合集,其实Power Query中生成的速度还是可以的(惰性运算),主要在加载上耗时较大,想象7000个不同对象中取两两组合的全部组合情况就多达2000万以上种组合。
认真你就输了,昨天我夜观星象也看到"sql旁门左道"有个小案例:
假设有个单列的员工表#table({"姓名"},List.Zip({{"畅心","施阳","海鲜","NTT","飞天篮球","玄月","小妖","兰色幻想"}}))
也做个两两组合吧:(SELECT A.姓名,B.姓名 as 名字 from [查询1] A,[查询1] B where A.姓名 < B.姓名)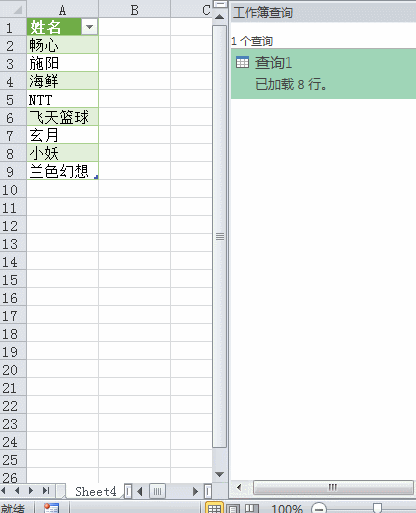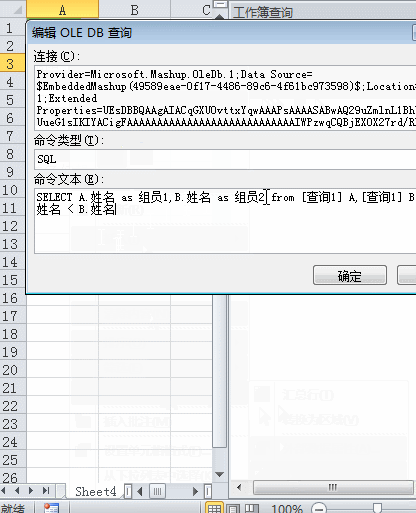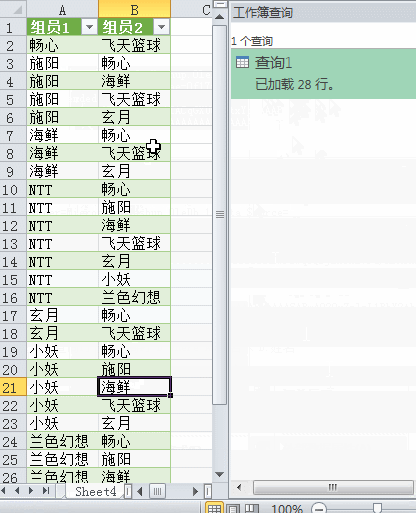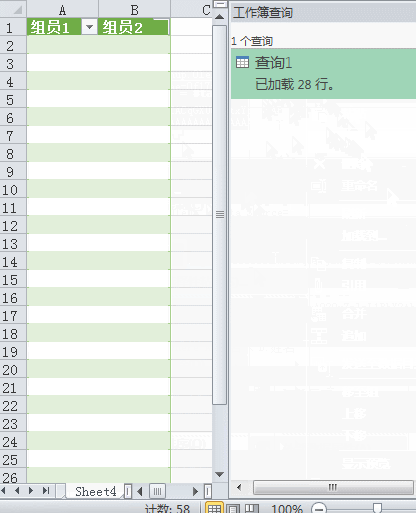
听说你们2016sql编辑命令框是灰色的,哈哈哈哈......
select * from [表1$] A,[表1$] B where A.姓名<B.姓名 order by A.姓名,B.姓名
如果取3个的组合就是:
select * from [表1$] A,[表1$] B,[表1$] C where A.姓名<B.姓名 and B.姓名<C.姓名 order by A.姓名,B.姓名,C.姓名然而这些都看得我脑壳痛,python给你做好了包,吃一个吧。
import itertools
a=['畅心','施阳','海鲜','篮球','小学生']
for x in itertools.product(a,a):
print(x[0],x[1])或者
import itertools
a=['畅心','施阳','海鲜','篮球','小学生']
print(list(itertools.product(a,a)))或者
a=['畅心','施阳','海鲜','篮球','小学生']
print([[x,y] for x in a for y in a])组合使用itertools.combinations,比如全组合输出:
import itertools
a=['畅心','施阳','海鲜','篮球','小学生']
b=[]
for i in range(1,6):
x=itertools.combinations(a,i)
b.append(list(x))
print(b)嵌套列表推导式做笛卡尔积:
[(x,y) for x in list1 for y in list2]笛卡尔活了,,,补一个当年学函数时候的旁门左道:BASE(row(1:25)-1,5,2)
{0;1;2;3;4}+10*{0,1,2,3,4}
听说最近开发的模糊匹配又是台破自行车?我还想用它做笛卡尔呢......


道高一尺 魔高一丈
https://pbihub.cn/users/44
自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)