PQ 大数运算基础篇

2020-08-12 15:49:42 ⋅ 2228 ⋅ 7 ⋅ 0

我们知道在excel中数字位数是有限制的，如果我们要进行大数运算该怎么办？
这里我用PQ来模拟了基础的笔算竖式思路：
首先来看最简单的两个大整数的加法：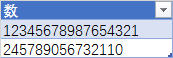
file

let
    源 = Excel.CurrentWorkbook(){[Name="表1"]}[Content],
    补位对齐 = [a=List.Sort(源[数],Text.Length),b=Text.PadStart(a{0},Text.Length(a{1}),"0"),c={b,a{1}}][c],
    按位逆序分组 = List.Reverse(List.Zip(List.Transform(补位对齐,each List.Transform(Text.ToList
(_),Number.From)))),
    模拟笔算进位 = List.Accumulate(按位逆序分组,{"",0},(x,y)=>[a=y{0}+y{1}+x{1},b={Text.From(Number.Mod(a,10))&x
{0},Byte.From(a>9)}][b]),
    最高位进位判断 = [T=模拟笔算进位,R=if 模拟笔算进位{1}=0 then 模拟笔算进位{0} else "1"&模拟笔算进位{0}][R]
in
    最高位进位判断

改写为函数形式：

let
    fx = (N1,N2)=>
let
    补位对齐 = [a=List.Sort({N1,N2},Text.Length),b=Text.PadStart(a{0},Text.Length(a{1}),"0"),c={b,a{1}}][c],
    按位逆序分组 = List.Reverse(List.Zip(List.Transform(补位对齐,each List.Transform(Text.ToList
(_),Number.From)))),
    模拟笔算进位 = List.Accumulate(按位逆序分组,{"",0},(x,y)=>[a=y{0}+y{1}+x{1},b={Text.From(Number.Mod(a,10))&x
{0},Byte.From(a>9)}][b]),
    最高位进位判断 = [T=模拟笔算进位,R=if 模拟笔算进位{1}=0 then 模拟笔算进位{0} else "1"&模拟笔算进位{0}][R]
in
    最高位进位判断
in  fx

或者将最高位进位判断放入迭代过程中：

let
    fx = (N1,N2)=>
let
    补位对齐 = [a=List.Sort({N1,N2},Text.Length),b=Text.PadStart(a{0},Text.Length(a{1}),"0"),c={b,a{1}}][c],
    按位逆序分组 = List.Reverse(List.Zip(List.Transform(补位对齐,each List.Transform(Text.ToList
(_),Number.From)))),
    模拟笔算进位 = List.Accumulate(按位逆序分组&{"畅心"},{"",0},(x,y)=>if y="畅心" then Text.Repeat("1",x{1})&x{0} else [a=y{0}+y{1}+x{1},b={Text.From(Number.Mod(a,10))&x
{0},Byte.From(a>9)}][b])
in
    模拟笔算进位
in  fx

扩展为多个大整数相加:

List.Accumulate(大整数列表,"0",fx)

多个大整数相加的完整代码可以写为：

let
    fx = (N1,N2)=>
let
    补位对齐 = [a=List.Sort({N1,N2},Text.Length),b=Text.PadStart(a{0},Text.Length(a{1}),"0"),c={b,a{1}}][c],
    按位逆序分组 = List.Reverse(List.Zip(List.Transform(补位对齐,each List.Transform(Text.ToList
(_),Number.From)))),
    模拟笔算进位 = List.Accumulate(按位逆序分组,{"",0},(x,y)=>[a=y{0}+y{1}+x{1},b={Text.From(Number.Mod(a,10))&x
{0},Byte.From(a>9)}][b]),
    最高位进位判断 = [T=模拟笔算进位,R=if 模拟笔算进位{1}=0 then 模拟笔算进位{0} else "1"&模拟笔算进位{0}][R]
in
    最高位进位判断
in  List.Accumulate(大整数列表,"0",fx)

当然多个大整数加法不需要后面的迭代处理，直接每个数逐位从低位向高位相加即可：

let
    fx = (大整数列表)=>
let
    补位对齐 = [a=List.Sort(大整数列表,{Text.Length,1}),b=List.Transform(大整数列表,each Text.PadStart(_,Text.Length(a{0}),"0"))][b],
    按位逆序分组 = List.Reverse(List.Zip(List.Transform(补位对齐,each List.Transform(Text.ToList
(_),Number.From)))),
    模拟笔算进位 = List.Accumulate(按位逆序分组,{"",0},(x,y)=>[a=List.Sum(y)+x{1},b={Text.From(Number.Mod(a,10))&x
{0},Number.RoundDown(a/10)}][b]),
    最高位进位判断 = [T=模拟笔算进位,R=if 模拟笔算进位{1}=0 then 模拟笔算进位{0} else Text.From(模拟笔算进位{1})&模拟笔算进位{0}][R]
in
    最高位进位判断
in
    fx     //如输出fx({"23135465654654654654987982132198658","99999999999999","32895487985269334899"})

或者

let
    fx = (大整数列表)=>
let
    按位逆序分组 = List.Reverse(List.Zip(List.Transform(大整数列表,each List.Transform(Text.ToList
(_),Number.From)))),
    模拟笔算进位 = List.Accumulate(按位逆序分组,{"",0},(x,y)=>[a=List.Sum(y)+x{1},b={Text.From(Number.Mod(a,10))&x
{0},Number.RoundDown(a/10)}][b]),
    最高位进位判断 = [T=模拟笔算进位,R=if 模拟笔算进位{1}=0 then 模拟笔算进位{0} else Text.From(模拟笔算进位{1})&模拟笔算进位{0}][R]
in
    最高位进位判断
in
    fx(List.Repeat({"99999999"},1000000))

进一步扩展大整数乘法
思路：其中一个数的每位数字与另一个数相乘返回多个大整数相加，多个大整数相加已经有函数，此步扩展只需解决其中一个大数的每位数字乘以另一个大数，生成一个大数列表即可！
由于是两个数相乘，转化为多个个位数与另一大数相乘上面fx可以改写为：

let
    fx1 = (个位数,N2)=>
let
    按位逆序分组 = List.Transform(List.Reverse(Text.ToList(N2)),each {Number.From(_),个位数}),
    模拟笔算进位 = List.Accumulate(按位逆序分组,{"",0},(x,y)=>[a=y{0}*y{1}+x{1},b={Text.From(Number.Mod(a,10))&x
{0},Number.RoundDown(a/10)}][b]),
    最高位进位判断 = [T=模拟笔算进位,R=if 模拟笔算进位{1}=0 then 模拟笔算进位{0} else Text.From(模拟笔算进位{1})&
模拟笔算进位{0}][R]
in
    最高位进位判断
in  fx1

由于其中一个数拆分为多个个位数与另一大数相乘生成多个大数，从低位到高位需要将每个生成大数后面进位在低位补0，所以上面fx1需要处理低位补0问题：
S=List.Zip({List.Reverse(Text.ToList(N1)),{0..Text.Length(N1)-1}})
多个个位数与另一大数相乘生成多个大数列表：

List.Transform(S,each fx1(_{0},N2)&Text.Repeat("0",_{1}))

也就是

大整数列表=List.Transform(List.Zip({List.Reverse(Text.ToList(N1)),{0..Text.Length(N1)-1}}),each fx1(NumberFrom(_{0}),N2)&Text.Repeat("0",_{1}))

最后多个大整数累加
List.Accumulate(大整数列表,"0",fx)
所以两个大整数相乘的完整代码可以写为：

let
    fx = (N1,N2)=>
let
    补位对齐 = [a=List.Sort({N1,N2},Text.Length),b=Text.PadStart(a{0},Text.Length(a{1}),"0"),c={b,a{1}}][c],
    按位逆序分组 = List.Reverse(List.Zip(List.Transform(补位对齐,each List.Transform(Text.ToList
(_),Number.From)))),
    模拟笔算进位 = List.Accumulate(按位逆序分组,{"",0},(x,y)=>[a=y{0}+y{1}+x{1},b={Text.From(Number.Mod(a,10))&x
{0},Byte.From(a>9)}][b]),
    最高位进位判断 = [T=模拟笔算进位,R=if 模拟笔算进位{1}=0 then 模拟笔算进位{0} else "1"&模拟笔算进位{0}][R]
in
    最高位进位判断,
fx1 = (个位数,N2)=>
let
    按位逆序分组 = List.Transform(List.Reverse(Text.ToList(N2)),each {Number.From(_),个位数}),
    模拟笔算进位 = List.Accumulate(按位逆序分组,{"",0},(x,y)=>[a=y{0}*y{1}+x{1},b={Text.From(Number.Mod(a,10))&x
{0},Number.RoundDown(a/10)}][b]),
    最高位进位判断 = [T=模拟笔算进位,R=if 模拟笔算进位{1}=0 then 模拟笔算进位{0} else Text.From(模拟笔算进位{1})&
模拟笔算进位{0}][R]
in
    最高位进位判断,
fun=(N1,N2)=>List.Accumulate(List.Transform(List.Zip({List.Reverse(Text.ToList(N1)),{0..Text.Length(N1)-1}}),each fx1(Number.From(_{0}),N2)&Text.Repeat("0",_{1})),"0",fx)
in  fun

尝试将fx和fx1写为一个函数：

let
    fx = (N1,N2,optional k)=>
let
    按位逆序分组 = if k=1 then List.Transform(List.Reverse(Text.ToList(N2)),each {Number.From(_),N1}) else 
    [补位对齐 = [a=List.Sort({N1,N2},Text.Length),b=Text.PadStart(a{0},Text.Length(a{1}),"0"),c={b,a{1}}][c],
    t = List.Reverse(List.Zip(List.Transform(补位对齐,each List.Transform(Text.ToList
(_),Number.From))))][t],
    模拟笔算进位 = List.Accumulate(按位逆序分组,{"",0},(x,y)=>[a=(if k=1 then y{0}*y{1} else y{0}+y{1})+x{1},b={Text.From(Number.Mod(a,10))&x
{0},Number.RoundDown(a/10)}][b]),
    最高位进位判断 = [T=模拟笔算进位,R=if 模拟笔算进位{1}=0 then 模拟笔算进位{0} else Text.From(模拟笔算进位{1})&
模拟笔算进位{0}][R]
in
    最高位进位判断,
fun=(M1,M2)=>List.Accumulate(List.Transform(List.Zip({List.Reverse(Text.ToList(M1)),{0..Text.Length(M1)-1}}),each fx(Number.From(_{0}),M2,1)&Text.Repeat("0",_{1})),"0",fx)
in  fun              //例如输出111111111^2                 fun("111111111","111111111")

然后可以扩展多个大整数乘法及带小数的乘法
多个大整数乘法可以写为：

let
    fx = (N1,N2,optional k)=>
let
    按位逆序分组 = if k=1 then List.Transform(List.Reverse(Text.ToList(N2)),each {Number.From(_),N1}) else 
    [补位对齐 = [a=List.Sort({N1,N2},Text.Length),b=Text.PadStart(a{0},Text.Length(a{1}),"0"),c={b,a{1}}][c],
    t = List.Reverse(List.Zip(List.Transform(补位对齐,each List.Transform(Text.ToList
(_),Number.From))))][t],
    模拟笔算进位 = List.Accumulate(按位逆序分组,{"",0},(x,y)=>[a=(if k=1 then y{0}*y{1} else y{0}+y{1})+x{1},b={Text.From(Number.Mod(a,10))&x
{0},Number.RoundDown(a/10)}][b]),
    最高位进位判断 = [T=模拟笔算进位,R=if 模拟笔算进位{1}=0 then 模拟笔算进位{0} else Text.From(模拟笔算进位{1})&
模拟笔算进位{0}][R]
in
    最高位进位判断,
fun=(M1,M2)=>List.Accumulate(List.Transform(List.Zip({List.Reverse(Text.ToList(M1)),{0..Text.Length(M1)-1}}),each fx(Number.From(_{0}),M2,1)&Text.Repeat("0",_{1})),"0",fx)
in  List.Accumulate(大整数列表,"1",fun)  
/*如输出List.Accumulate({"445333448676768","54545656789","645666666"},"1",fun)*/

小数处理：

let
    fx = (N1,N2,optional k)=>
let
    按位逆序分组 = if k=1 then List.Transform(List.Reverse(Text.ToList(N2)),each {Number.From(_),N1}) else 
    [补位对齐 = [a=List.Sort({N1,N2},Text.Length),b=Text.PadStart(a{0},Text.Length(a{1}),"0"),c={b,a{1}}][c],
    t = List.Reverse(List.Zip(List.Transform(补位对齐,each List.Transform(Text.ToList
(_),Number.From))))][t],
    模拟笔算进位 = List.Accumulate(按位逆序分组,{"",0},(x,y)=>[a=(if k=1 then y{0}*y{1} else y{0}+y{1})+x{1},b={Text.From(Number.Mod(a,10))&x
{0},Number.RoundDown(a/10)}][b]),
    最高位进位判断 = [T=模拟笔算进位,R=if 模拟笔算进位{1}=0 then 模拟笔算进位{0} else Text.From(模拟笔算进位{1})&
模拟笔算进位{0}][R]
in
    最高位进位判断,
fun=(M1,M2)=>List.Accumulate(List.Transform(List.Zip({List.Reverse(Text.ToList(M1)),{0..Text.Length(M1)-1}}),each fx(Number.From(_{0}),M2,1)&Text.Repeat("0",_{1})),"0",fx)
in  [L=大数列表,
     T=List.Transform(L,each Text.Remove(_,".")),
     N=List.Sum(List.Transform(L,each Text.Length(Text.Split(_,"."){1}?))),
     S=List.Accumulate(T,"1",fun),
     S1=if N=null then S else Text.Insert(S,Text.Length(S)-N,".")][S1]

当然上面没有优化处理小数点后可以省略的0的情况，如"123.00","123.050"，可以trim处理下首尾无效0，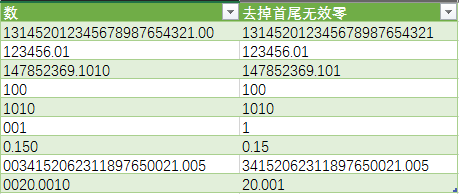
file
另外加法带小数处理类似不再赘述，乘法如果有负数、只需全部取绝对值相乘、最后前面的符号问题根据负号的个数奇偶判断（不考虑-0这种写法）
然后可以扩展减法问题，减法即为加负数...
两个数相加就分为三大类情况：两个正数相加、一正一负相加、两个负数相加（0可以算为正数）
两个正数算法已经知道、两个负数只需要转为两个正数相加后前面补负号即可，现在主要处理一正一负情况。
一正一负牵涉正负数前后顺序两种情况：

let
fx=(N1,N2)=>
let
    定位= List.Sort({N1,N2},each Text.PadStart(Text.Remove(_,"-"),99,"0")),
    逆序分组=List.Zip(List.Transform(定位,each List.Reverse(List.Transform(Text.ToList(Text.Remove(_,"-")),Number.From)))),
    模拟减法=List.Accumulate(逆序分组,{"",0},(x,y)=>{Text.From(y{1}-List.Sum({y{0},x{1}})+10*Byte.From(y{1}<List.Sum({y{0},x{1}})))&x{0},Byte.From(List.Sum({y{0},x{1}})>y{1})}),
    处理高位0=if Text.Trim(模拟减法{0},"0")="" then "0" else Text.Trim(模拟减法{0},"0"),
    判断符号=(if Text.Start(定位{1},1)="-" and 处理高位0<>"0" then "-" else "")&处理高位0
in
    判断符号
in
fx

此时回过头来看两个正大整数加法在补位对齐那一步就可以省略，只是zip后面需要处理null值，改写为：

let
    fx = (N1,N2)=>
let
    按位逆序分组 = List.Zip(List.Transform({N1,N2},each List.Reverse(List.Transform(Text.ToList
(_),Number.From)))),
    模拟笔算进位 = List.Accumulate(按位逆序分组,{"",0},(x,y)=>[a=List.Sum(y)+x{1},b={Text.From(Number.Mod(a,10))&x
{0},Byte.From(a>9)}][b]),
    最高位进位判断 = [T=模拟笔算进位,R=if 模拟笔算进位{1}=0 then 模拟笔算进位{0} else "1"&模拟笔算进位{0}][R]
in
    最高位进位判断
in  fx

进一步将两个负大整数的加法融入上面两个正大整数加法里面只需最后判断符号：

let
    fx = (N1,N2)=>
let
    逆序分组 = List.Zip(List.Transform({N1,N2},each List.Reverse(List.Transform(Text.ToList
(Text.Remove(_,"-")),Number.From)))),
    模拟笔算进位 = List.Accumulate(逆序分组,{"",0},(x,y)=>[a=List.Sum(y)+x{1},b={Text.From(Number.Mod(a,10))&x
{0},Byte.From(a>9)}][b]),
    最高位进位判断 = [T=模拟笔算进位,R=if 模拟笔算进位{1}=0 then 模拟笔算进位{0} else "1"&模拟笔算进位{0}][R],
    判断符号=(if Text.Start(N1,1)="-" and Text.Start(N2,1)="-" then "-" else "")&最高位进位判断
in
    判断符号
in  fx

file

道高一尺魔高一丈
https://pbihub.cn/users/44

PQ 大数运算基础篇

Power Query驾驶指南

作者：畅心

专栏推荐

PQ 大数运算基础篇

添加附言

Power Query驾驶指南

作者：畅心

专栏推荐