约瑟夫环

约瑟夫环破解应该在我15岁左右,那时第一次看见这个游戏如此神奇,后来花了3小时破解了解法,那时我还不会写程序,现在我会了
将15岁时的解法全部公之于众

= List.Accumulate(List.Reverse({1..13}),{},(x,y)=>if x={} then {y}&x else if  List.Count(x)=1 then x&{y} else List.LastN(x,1)&{y}&List.RemoveLastN(x,1) )

解题:
一堆牌,有N 张,把上面一张放最下面,再把最上面的一张牌拿出,
重复这个动作,直到结束为止,最后的新序列要是一个有序的表
比如N=13,结果是:{1..13},1代表第一张拿出的牌,现在我们模拟一下原来序列
{13}序列未知,实际上它有序列的,结果{1..13}
假设一张牌
{1} -{}=>{},{1} 直接移动到另一个表
{2,1}--{}=>{2}--{1}=>{}---{1,2}
{2,1,3}--{}=>{3,2}--{1}=>{3}--{1,2}=>{}--{1,2,3}
看了简直蒙了
现在我们退回去
{},{1,2,3}=>{3}-{1,2}=>{3,2}-{1}=>{2,1,3}--{}

上面的问题解决了一张牌的出栈问题
面对多次如何解决,就是每次从上面拿一张牌放最底下,再弹出一张,上面已经解决了
如果我要从上面拿五张牌放底下,如何处理呢,同样简单

= let fx=(t,n )=>if n=0  then t else @fx(List.LastN(t,1)&List.RemoveLastN(t,1),n-1) ,  
       fn=(u,v) => List.Accumulate(List.Reverse({1..u}),{},(x,y)=>[m={y}&x,q=fx(m,v)][q]) 
  in fn(13,5)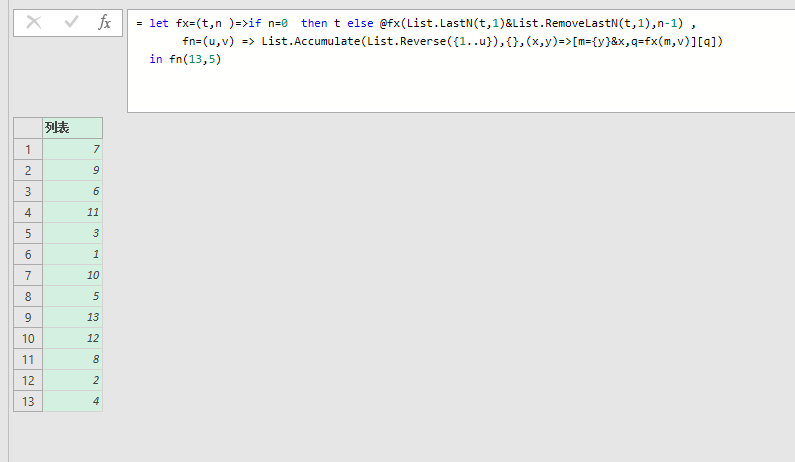

就这么简单
现在我调用一下
fn(13,1)结果如何呢: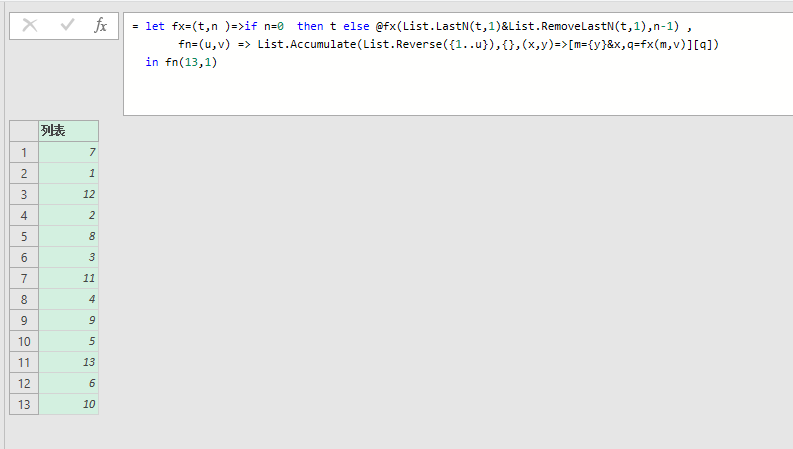

这个就是上面的演示文件
fn(10,3)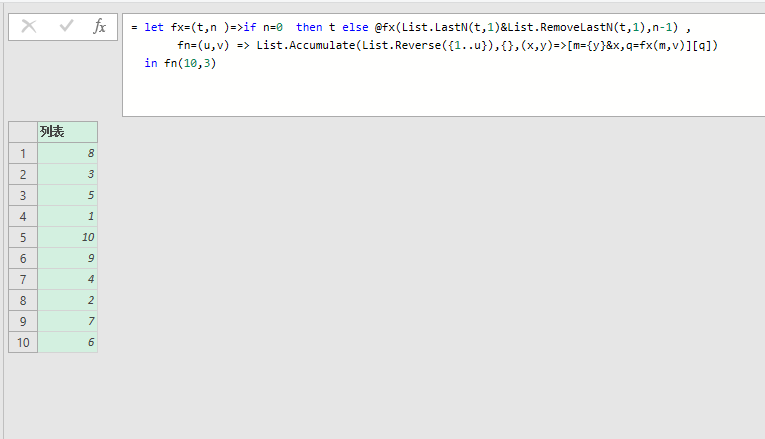

fn(20,10)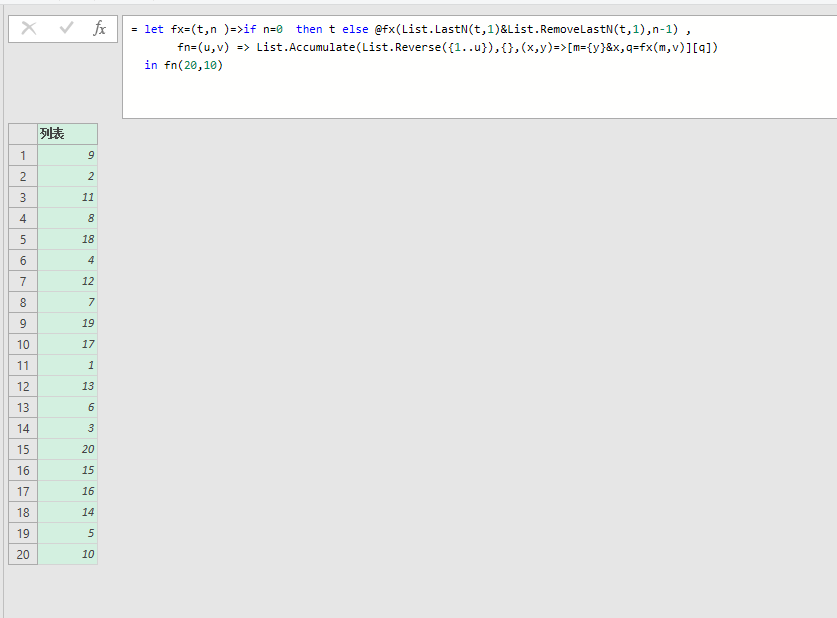

fn(5,10)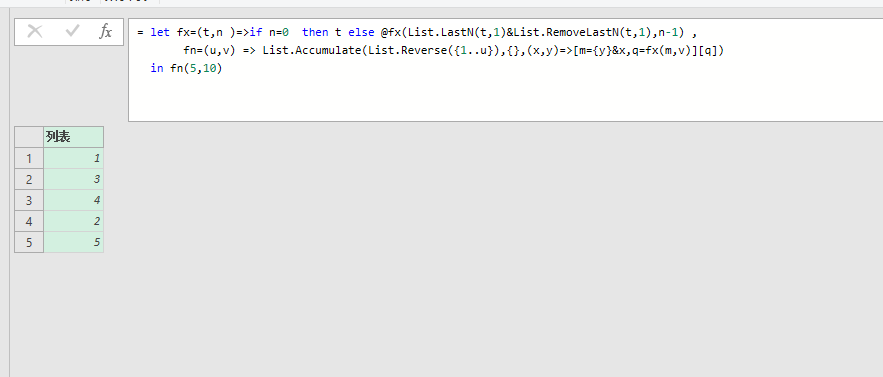

大家一定会差异,为什么如此神奇
后续会增加难度

= List.Generate(()=>{13,{}},each _{0}>=0 ,each {_{0}-1,[a={_{0}}&_{1},b=List.LastN(a,1)&List.RemoveLastN(a,1)][b]},each _{1}){13}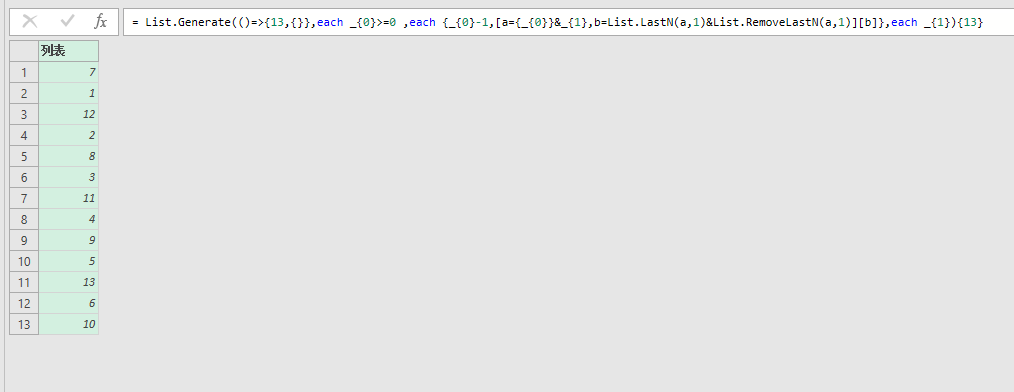

= let fx=(x)=>List.Generate(()=>[a=x,b={}],each [a]>=0,each [a=[a]-1,r= {[a]}&[b],b=List.LastN(r,1)&List.RemoveLastN(r,1)],each [b]){x} in fx(13)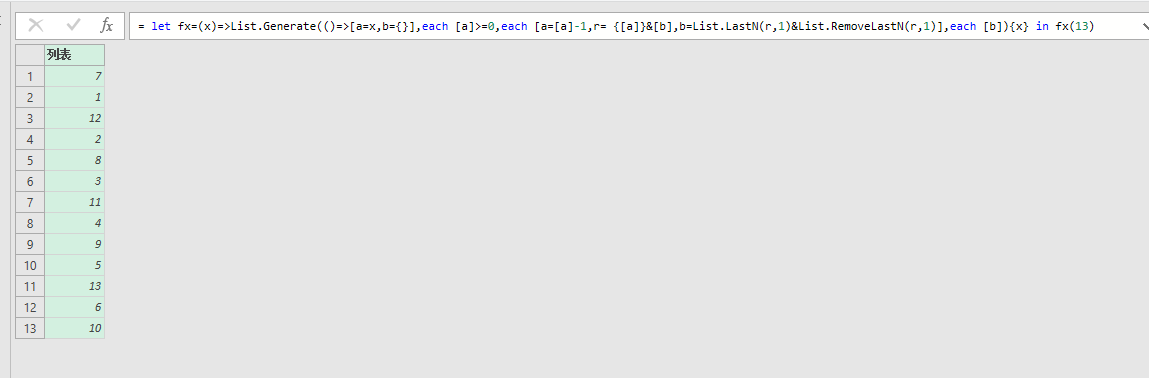

很多看官可能已经发现了问题,说这个和约瑟夫环没有关系吧 其实有关系的

= let    fx=(x,n)=>if n=1 then x else @fx(List.Skip(x)&{x{0}},n-1) ,
         fn=(t,s)=> List.Accumulate({1..t},{{},{1..t}},(x,y)=>[a= fx(x{1},s),c ={x{0}&{a{0}},List.Skip(a)}][c]){0}  
   in    fn(13,5)

fn(13,5)什么意思呢?就是13个人,数数,数到5就拉去枪毙,计算枪毙的序号,假设每个犯人都编了号1,2,3...13
fx(x,5)代表5循环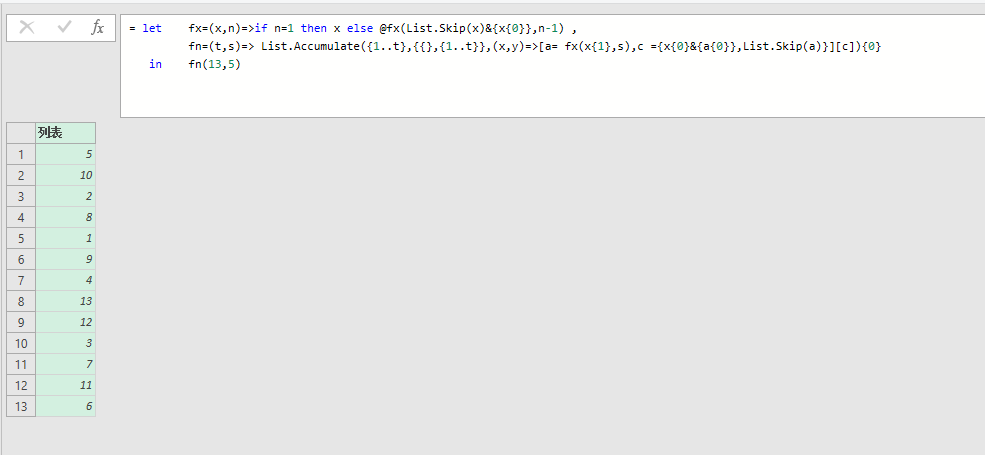

我们可以随便条件参数试试
比如fn(100,20)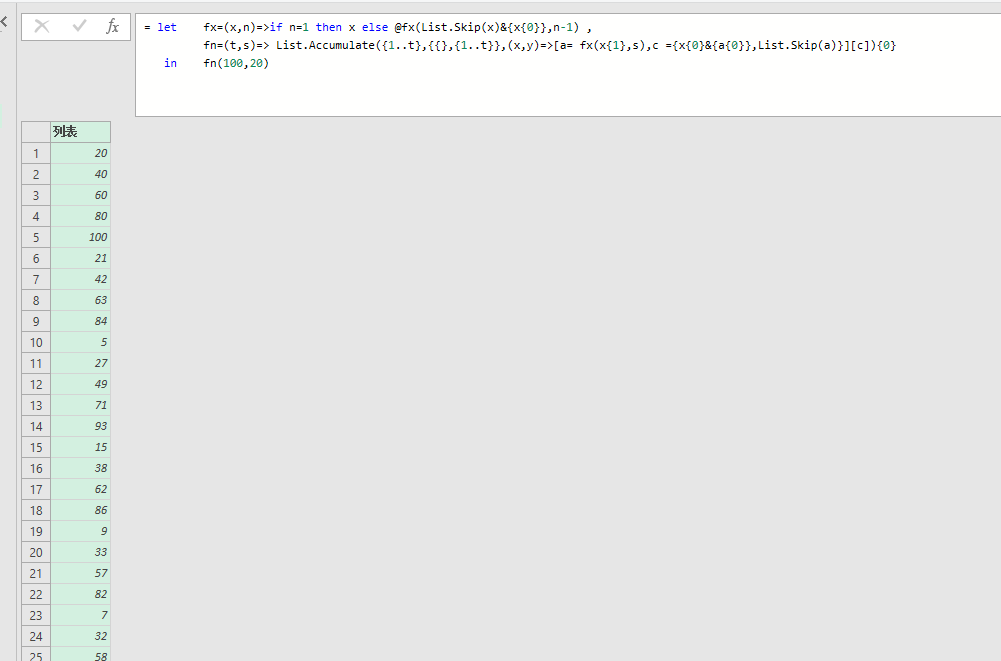

fn(10,3)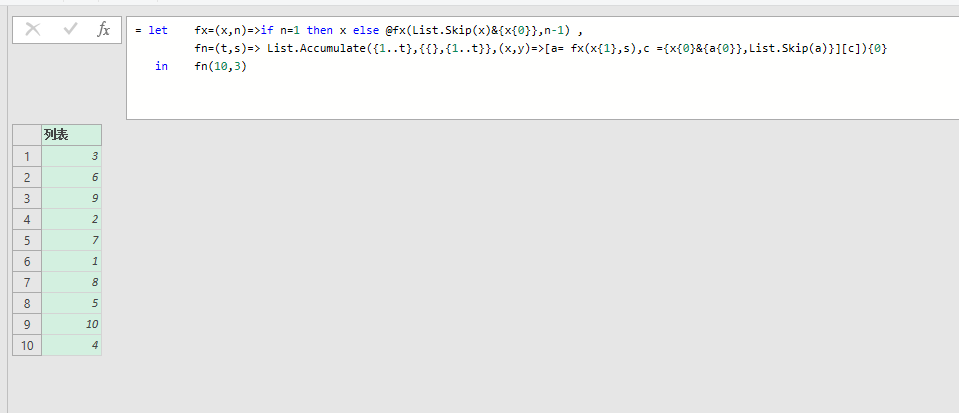

有兴趣的可以去验证一下
是不是很好玩